Liquefaction Characteristics
Liquefaction is the loss of shear strength in saturated cohesionless soils that are subjected to a dynamic load (Coduto, 1999). As a dynamic load is placed upon a saturated cohesionless soil the pore water pressure rises and, as a result, the effective stress reduces. This occurrence is based on the fact that effective stress is equal to the total stress minus the pore water pressure (Craig, 1997).
Liquefaction is the loss of shear strength in saturated cohesionless soils that are subjected to a dynamic load (Coduto, 1999). As a dynamic load is placed upon a saturated cohesionless soil the pore water pressure rises and, as a result, the effective stress reduces. This occurrence is based on the fact that effective stress is equal to the total stress minus the pore water pressure (Craig, 1997).
If the effective stress reduces to zero, the soil has no shear strength and develops into a liquid-like state. The specific way in which the soil liquefies is greatly dependent upon the initial relative density (i.e. whether loose or dense) (López-Queroln and Blázquez, 2006).
There are two main types of liquefaction (Coduto, 1999):
Flow Liquefaction
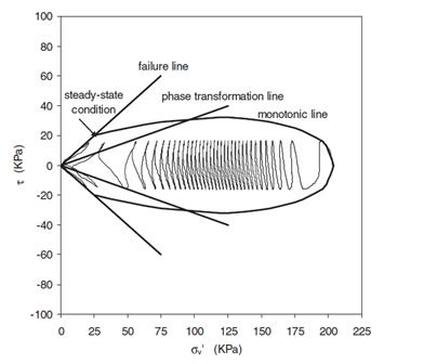
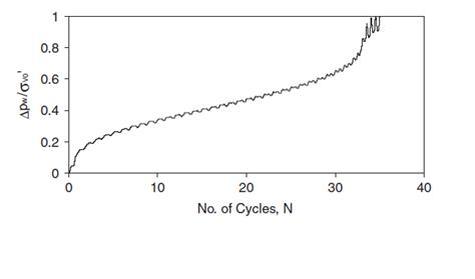
Loose sands, when exposed to shear will decrease in volume and as dynamic loading occurs quickly, the pore water is unable to drain away. This therefore will create an increase in the pore water pressure and consequently a reduction in effective stress (Craig, 1997). Figures 1 and 2 below show the stress path to failure for a loose sand sample subjected to cyclic loading and the excess pore water pressure build up respectively (López-Queroln and Blázquez, 2006). As can be seen in figure 1 and 2 there is a progressive loss in shear strength with each cycle which coincides with an increase in excess pore water that also occurs with every cycle. The sample starts with a effective stress of 200kPa and a cyclic load with a CSR (ratio of maximum cyclic shear stress to initial effective confining stress) equal to 0.08 is applied. When this cyclic load is applied the shear stress in the sand sample increases and as a result the sand sample starts to contract. This contraction increases the pore water pressure, therefore decreasing the effective stress. As the sample is unloaded and subsequently loading in the other direction the sand sample continues to contract. This excess pore water pressure is still unable to drain away due to the fact that the loading is occurring quickly. This causes progressive loss in effective stress and progressive gain in excess pore water pressure cycle by cycle. Eventually the applied shear stress is greater than the shear resistance of the sample and failure will occur. This type of liquefaction is known as flow liquefaction.
There are two main types of liquefaction (Coduto, 1999):
- Flow Liquefaction occurs in loose saturated sands and generally leads to sudden large shear movements.
- Cyclic Mobility occurs in medium to dense saturated sands, the shear movements in this type of liquefaction are not generally as dramatic as flow liquefaction as cyclic mobility produces incremental shear movements.
Flow Liquefaction
Loose sands, when exposed to shear will decrease in volume and as dynamic loading occurs quickly, the pore water is unable to drain away. This therefore will create an increase in the pore water pressure and consequently a reduction in effective stress (Craig, 1997). Figures 1 and 2 below show the stress path to failure for a loose sand sample subjected to cyclic loading and the excess pore water pressure build up respectively (López-Queroln and Blázquez, 2006). As can be seen in figure 1 and 2 there is a progressive loss in shear strength with each cycle which coincides with an increase in excess pore water that also occurs with every cycle. The sample starts with a effective stress of 200kPa and a cyclic load with a CSR (ratio of maximum cyclic shear stress to initial effective confining stress) equal to 0.08 is applied. When this cyclic load is applied the shear stress in the sand sample increases and as a result the sand sample starts to contract. This contraction increases the pore water pressure, therefore decreasing the effective stress. As the sample is unloaded and subsequently loading in the other direction the sand sample continues to contract. This excess pore water pressure is still unable to drain away due to the fact that the loading is occurring quickly. This causes progressive loss in effective stress and progressive gain in excess pore water pressure cycle by cycle. Eventually the applied shear stress is greater than the shear resistance of the sample and failure will occur. This type of liquefaction is known as flow liquefaction.
Figure 1 - (Initial confining pressure 200kPa, CSR=0.8) stress path of a loose saturated sand subjected to cyclic loading
Figure 2 – Excess pore water pressure for loose saturated sand subjected to cyclic loading
Cyclic Mobility
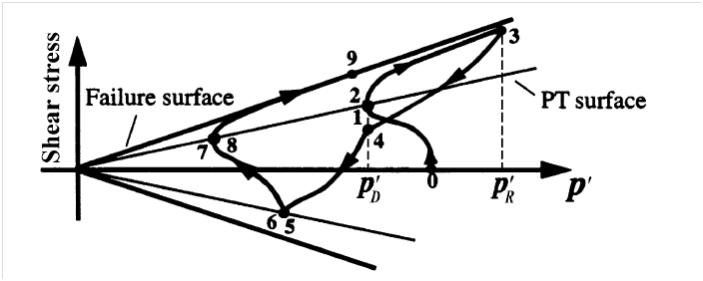
In a dense cohesionless soil there exists significant interlocking between particles, that must necessarily be overcome before shear failure can take place (Craig, 1997). When a saturated cohesionless soil specimen is subjected to shear the soil will initially contract during loading. However, as the interlocking forces are overcome there will be an increase in volume as the specimen starts dilate (Craig, 1997). This processes of contraction then subsequently dilation therefore creates a more complex liquefaction. Figure 3 below shows the failure path of dense sand (Elgamal et al., 2003). As a shear stress is applied, between phases 0 and 1 there is a tendency for contraction in the sand, therefore the pore water pressure increases resulting in a decrease in effective stress. As the failure path reaches the Phase Transformation Surface (PT Surface) there is a switch from contractive to dilative behaviour. With this dilation (between phase 2 and 3) there is a reduction in pore water pressure and the effective stress increases and consequently the shear strength increases. As unloading occurs (or loading in the opposite direction) the sand will have the tendency to contract again. This constant fluctuation between contractive and dilation behaviours causes the sand to continuously strengthen and weaken, this process is referred to as cyclic mobility (Elgamal, et al., 2003; Lopez-Queroln & Blazquez, 2006).
Cyclic Mobility
In a dense cohesionless soil there exists significant interlocking between particles, that must necessarily be overcome before shear failure can take place (Craig, 1997). When a saturated cohesionless soil specimen is subjected to shear the soil will initially contract during loading. However, as the interlocking forces are overcome there will be an increase in volume as the specimen starts dilate (Craig, 1997). This processes of contraction then subsequently dilation therefore creates a more complex liquefaction. Figure 3 below shows the failure path of dense sand (Elgamal et al., 2003). As a shear stress is applied, between phases 0 and 1 there is a tendency for contraction in the sand, therefore the pore water pressure increases resulting in a decrease in effective stress. As the failure path reaches the Phase Transformation Surface (PT Surface) there is a switch from contractive to dilative behaviour. With this dilation (between phase 2 and 3) there is a reduction in pore water pressure and the effective stress increases and consequently the shear strength increases. As unloading occurs (or loading in the opposite direction) the sand will have the tendency to contract again. This constant fluctuation between contractive and dilation behaviours causes the sand to continuously strengthen and weaken, this process is referred to as cyclic mobility (Elgamal, et al., 2003; Lopez-Queroln & Blazquez, 2006).
Figure 3 - Stress path to failure for dense saturated sand
References
Coduto, D. P., 1999. Geotechnical Engineering Principles and Practices. New Jersey: Prentice-Hall.
Craig, R., 1997. Soil Mechanics. 6th Edition. London: E & FN Spon.
Elgamal, A., Yang, Z., Parra, E. and Regheb, A., 2003. Modeling of Cyclic Mobility in Saturated Cohesionless Soils. International Journal of Plasicity, Issue 19, pp. 883-905.
López-Queroln, S. and Blázquez, R., 2006. Liquefaction and cyclic mobility model for saturated granular media. International Journal for Numerical and Analytical Methods in Geomechanics, Issue 30, pp. 413-439.
Figures courtesy of:
Figure 1: López-Queroln and Blázquez, 2006
Figure 2: López-Queroln and Blázquez, 2006
Figure 3: Elgamal, et al., 2003